lunes, 23 de noviembre de 2015
martes, 3 de noviembre de 2015
BIOGRAFÍA: Thomas Bayes (1702-1761)
Aportado por Aurora Távora García
THOMAS BAYES (Reino Unido, 1702-1761)Thomas Bayes fue uno de los primeros en utilizar la probabilidad inductivamente y establecer una base matemática para la inferencia probabilísticaSe conocen pocos datos de su vida, incluso es dudoso el año de su nacimiento. Estudió teología en la universidad de Edimburgo. Fue ministro presbiteriano, no se casó y se salió de ministro. Llevó una vida tranquila dedicada a sus actividades científicas, entre ella las matemáticas, inferencia estadística y teología.
En 1731 escribió el tratado religioso “la divina benevolencia, o un intento de probar que el principal fin de la providencia divina es la felicidad de sus criaturas”.En 1734 el obispo George Berkeley ataca al cálculo diferencial de Newton pues indicaba que dichos fundamentos no eran más evidentes que la religión cristiana. Entre las réplicas a Berkeley, aparece una en 1736 firmada por Bayes bajo el pseudónimo de John Noon con el título “Una introducción a la teoría de los fluxiones y una defensa de los matemáticos contra las objeciones del autor del analista”. Son los únicos dos tratados que se conoce que publicara en vida. Demuestra algunos teoremas básicos relativos al cálculo con los diferenciales.Dos años después de su muerte se le envió a la Royal Society la obra la cual sería más importante hecha por él. “Un ensayo hacia la solución de un problema de la doctrina de probabilidades” En este presenta el siguiente problema: “dado el número de veces que un suceso ha ocurrido y no se ha presentado, calcular la probabilidad de que se presente en una sola repetición y esté comprendido entre dos valores de probabilidad conocidos”El teorema que lleva su nombre se refiere a la probabilidad de un suceso condicionado por la ocurrencia de otro suceso. Más específicamente, con su teorema se resuelve el problema conocido como " la probabilidad inversa".
THOMAS BAYES (Reino Unido, 1702-1761)Thomas Bayes fue uno de los primeros en utilizar la probabilidad inductivamente y establecer una base matemática para la inferencia probabilísticaSe conocen pocos datos de su vida, incluso es dudoso el año de su nacimiento. Estudió teología en la universidad de Edimburgo. Fue ministro presbiteriano, no se casó y se salió de ministro. Llevó una vida tranquila dedicada a sus actividades científicas, entre ella las matemáticas, inferencia estadística y teología.
En 1731 escribió el tratado religioso “la divina benevolencia, o un intento de probar que el principal fin de la providencia divina es la felicidad de sus criaturas”.En 1734 el obispo George Berkeley ataca al cálculo diferencial de Newton pues indicaba que dichos fundamentos no eran más evidentes que la religión cristiana. Entre las réplicas a Berkeley, aparece una en 1736 firmada por Bayes bajo el pseudónimo de John Noon con el título “Una introducción a la teoría de los fluxiones y una defensa de los matemáticos contra las objeciones del autor del analista”. Son los únicos dos tratados que se conoce que publicara en vida. Demuestra algunos teoremas básicos relativos al cálculo con los diferenciales.Dos años después de su muerte se le envió a la Royal Society la obra la cual sería más importante hecha por él. “Un ensayo hacia la solución de un problema de la doctrina de probabilidades” En este presenta el siguiente problema: “dado el número de veces que un suceso ha ocurrido y no se ha presentado, calcular la probabilidad de que se presente en una sola repetición y esté comprendido entre dos valores de probabilidad conocidos”El teorema que lleva su nombre se refiere a la probabilidad de un suceso condicionado por la ocurrencia de otro suceso. Más específicamente, con su teorema se resuelve el problema conocido como " la probabilidad inversa".
ESTADÍSTICA CON HUMOR: lo que las mujeres dicen, piensan y hacen
Aportado por Alba Trujillo Aguilar
Esta viñeta muestra
la probabilidad de la intersección de que ocurran A, B y C con la siguiente
frase: “Bien, vamos a continuar con los sucesos, hoy vamos a ver el concepto
del suceso intersección”.
Se denomina suceso
intersección de A,B y C al formado por los resultados experimentales que están
simultáneamente en A, B y C
El suceso A es “lo
que las mujeres piensan”; B, “lo que las mujeres hacen”; y por último, el
suceso C, “lo que las mujeres dicen”. El resultado de la intersección de estos
tres sucesos es el conjunto vacío, es decir, imposible.
BIOGRAFÍA: William Sealy Gosset (1876-1937)
Aportado por Beatriz Gómez
William
Sealy Gosset nació en Canterbury (Inglaterra) en junio de 1876, era hijo de
Agnes Sealy y el coronel Frederic Gosset. Asistió a la escuela Winchester
College (donde luego acabaría siendo profesor), y más tarde estudio química y
matemáticas en el New College de Oxford.
En
1899 tras graduarse, se incorporó a trabajar en la famosa compañía Cervera
Guinnes de Dublin en el departamento de fermentación. Para poder realizar su
trabajo y encontrar los mejores materiales con los que realizar el producto dentro
de la empresa, Gosset constató la necesidad estadística de desarrollar un método correcto para el tratamiento de
muestras pequeñas que daría lugar a su gran descubrimiento. Para desarrollar
este método acudió al laboratorio de su
compañero Karl Pearson y principalmente utilizó como herramientas la “Teoría de
errores de observaciones” y el “Método de mínimos cuadrados”
Para
evitar que se filtrara información confidencial de la empresa, Guinnes prohibió
a sus trabajadores la publicación de artículos, por lo que Gosset tuvo que
buscar un pseudónimo para publicar su trabajo, este pseudónimo seria “STUDENT”,
que daría nombre a la gran aportación que Gosset hizo al campo de la
estadística, la distribución de t-Student que hemos estudiado en clase.
Finalmente
falleció a los 61años de edad en octubre de 1937.
BIOGRAFÍA: Ronald Aylmer Fisher (1890-1962)
Aportado por Ana Cristina Barroso Ruiz
Introdujo el concepto
de aleatoriedad y las técnicas de análisis de la varianza.
(Londres, 1890-Adelaida, Australia, 1962). Matemático y biólogo británico.
Se graduó por la Universidad de Cambridge en 1912. Pionero en la aplicación de
métodos estadísticos al diseño de experimentos científicos, en 1919 comenzó a
trabajar en la estación experimental de Rothamsted, donde realizó trabajos
estadísticos relacionados con la reproducción de las plantas. Desarrolló
técnicas para obtener mayor cantidad de información útil a partir de muestras
de datos más pequeñas, introdujo el principio de aleatoriedad en la recogida de
muestras y el análisis de la varianza o análisis multivariacional. Publicó su
metodología estadística en 1925 en Methods for Research Workers. Trasladó sus
investigaciones al campo de la genética en The Genetical Theory of Natural Selection
(1930), que resume sus puntos de vista sobre la eugenesia y el papel de control
que ejercen los genes sobre los caracteres dominantes, y en el que considera la
selección como la fuerza directriz de la evolución, más que la mutación. En
1933 ocupó la cátedra Galton de eugenesia en la Universidad de Londres, y de
1943 a 1957, la cátedra Balfour de genética en la Universidad de Cambridge. Los
últimos años de su vida los pasó trabajando para la Commonwealth Scientific and
Industrial Research Organization en Adelaida.BIOGRAFÍA : Diego Ollero y Carmona (1839-1907)
Aportado por Elena Panadero
Nació en Porcuna (Jaén) en
1839 e ingresó en el Real Colegio de Artillería de Segovia a los catorce años.
Participó en la guerra civil de 1875 y ocupó puestos importantes donde eran
necesarios grandes conocimientos técnicos de artillería.
Fue profesor en la Academia
de Artillería, vocal de la Junta Superior Facultativa, en cuyo destino
participó en numerosas Comisiones nacionales y en el extranjero, académico de
ciencias y gran balístico.
Famoso dentro del rubro de la
estadística por su Tratado de Cálculo de
Probabilidades; el cual constituye el primer manual moderno en castellano
sobre probabilidades donde se hace uso del cálculo diferencial.
Este manual desarrolla en 5
capítulos una explicación matemática necesaria para el entendimiento del
Tratado, unos principios fundamentales de probabilidad, un capítulo entero dedicado
al teorema de Bernoulli, un estudio de la teoría estadística del análisis de
errores y una exposición del método de los mínimos cuadrados.
Este Tratado plantea una
metodología y una aplicación de herramientas matemáticas, las cuales se
asemejan a as principales publicaciones modernas sobre el cálculo de
probabilidad de países como Inglaterra, Francia, etc.
BIOGRAFÍA: Carl Friedrich Gauss (1777-1855)
Aportado por Irene del Castillo Fuentes y Marta Caballero Morales
Encuadramos
esta reflexión dentro de la estadística
inferencial; que es aquella que se dedica a la generación de los
modelos, inferencias y predicciones asociadas a los fenómenos en cuestión.
Johann
Carl Friedrich Gauss ( Brunswik, 30 de abril de 1777- Gotinga, 23 de febrero de
1855). Matemático, astrónomo, geodesta y físico alemán que contribuyó en la
teoría de los números, el análisis matemático, la geometría diferencial, la
estadística, el álgebra.
Encuadramos
esta reflexión dentro de la estadística
inferencial; que es aquella que se dedica a la generación de los
modelos, inferencias y predicciones asociadas a los fenómenos en cuestión.
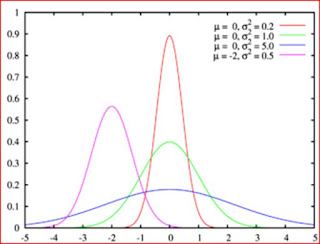
La
distribución normal que Gauss define es una de las distribuciones de
probabilidad de variable continua que con más frecuencia aparece aproximada en
fenómenos reales.
La
gráfica de su función de densidad tiene una forma acampanada y es simétrica
respecto de un determinado parámetro estadístico. Se conoce como campana de
Gauss y es el gráfico de una función gaussiana.
La
importancia que todo esto tiene es que permite modelar numerosos fenómenos
naturales sociales y psicológicos.
Podemos observar que la línea verde
corresponde a la distribución normal estándar.
La distribución normal también aparece en
muchas áreas de la propia estadística. Por ejemplo la distribución muestral de
las medias muestrales es aproximadamente normal aunque la distribución de la
población de la cual se extrae la muestra no lo sea.
La distribución está caracterizada por dos
parámetros: la media, μ y la desviación típica.
La media la interpretaremos como un factor de la traslación;
mientras que la desviación típica como un factor de escala, grado de
dispersión…
COMENTARIO NOTICIA: Un modelo probabilístico calcula la mejor localización de un parque eólico
La noticia del SINC (Servicio de Información y Noticias
Científicas) nos muestra una vez más la aplicación real de la Estadística a
nuestro día a día. Un equipo compuesto de un español y dos americanos presentó
en la Intertional Joint Conference on Artificial Intelligence (IJCAI'15)
celebrada en Buenos Aires, un nuevo modelo probabilístico que calcularía la
mejor localización de los parques eólicos.
El muestreo se realizó con anemómetros (instrumentos para
medir la velocidad del viento) colocados en el Museo de Ciencias de Cambridge
(Massachusetts). A diferencia del método habitual, sólo hacen falta 3 meses de
recogida de datos, a diferencia de los 8-12 de los modelos anteriores.
Esta nueva estimación surgió al saberse que los modelos
utilizados hasta ahora seguían la hipótesis de que la distribución de los datos
obtenidos formaban una Campana de Gauss, es decir, datos que suponían seguir
una distribución normal. Este nuevo modelo, utiliza unas distribuciones que
modifican la forma de la campana demostrando una
mejoría en la precisión de los resultados. Para tener en cuenta los casos
extremos (mucho o poco viento), decidieron incorporar al modelo una técnica
que tuviera en cuenta dichos casos extremos (funciones de Cópulas no
Gaussianas) mejorando así los resultados.
Lo que llamó la atención de este nuevo hallazgo fue la
simplificación del proceso de muestreo en tiempo y el bajo coste que supuso la
obtención de datos, por ser información de aeropuertos (de dominio público).
Suscribirse a:
Entradas (Atom)