Johann
Carl Friedrich Gauss ( Brunswik, 30 de abril de 1777- Gotinga, 23 de febrero de
1855). Matemático, astrónomo, geodesta y físico alemán que contribuyó en la
teoría de los números, el análisis matemático, la geometría diferencial, la
estadística, el álgebra.
Encuadramos
esta reflexión dentro de la estadística
inferencial; que es aquella que se dedica a la generación de los
modelos, inferencias y predicciones asociadas a los fenómenos en cuestión.
La
distribución normal que Gauss define es una de las distribuciones de
probabilidad de variable continua que con más frecuencia aparece aproximada en
fenómenos reales.
La
gráfica de su función de densidad tiene una forma acampanada y es simétrica
respecto de un determinado parámetro estadístico. Se conoce como campana de
Gauss y es el gráfico de una función gaussiana.
La
importancia que todo esto tiene es que permite modelar numerosos fenómenos
naturales sociales y psicológicos.
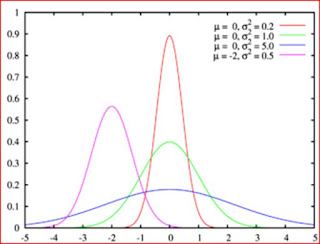
Podemos observar que la línea verde
corresponde a la distribución normal estándar.
La distribución normal también aparece en
muchas áreas de la propia estadística. Por ejemplo la distribución muestral de
las medias muestrales es aproximadamente normal aunque la distribución de la
población de la cual se extrae la muestra no lo sea.
La distribución está caracterizada por dos
parámetros: la media, μ y la desviación típica.
La media la interpretaremos como un factor de la traslación;
mientras que la desviación típica como un factor de escala, grado de
dispersión…
No hay comentarios:
Publicar un comentario